In Part 1 of Introduction to Neural Networks, we covered the McCulloch-Pitts (M-P) neuron, which is a simple artificial neuron. However, the M-P neuron has a limitation as it does not involve any learning process and the weights need to be set manually. In this article, we will explore an improvement called the Perceptron, which can learn the weights over time. We will also learn how to train a Perceptron from scratch to classify logical operations such as AND or OR.

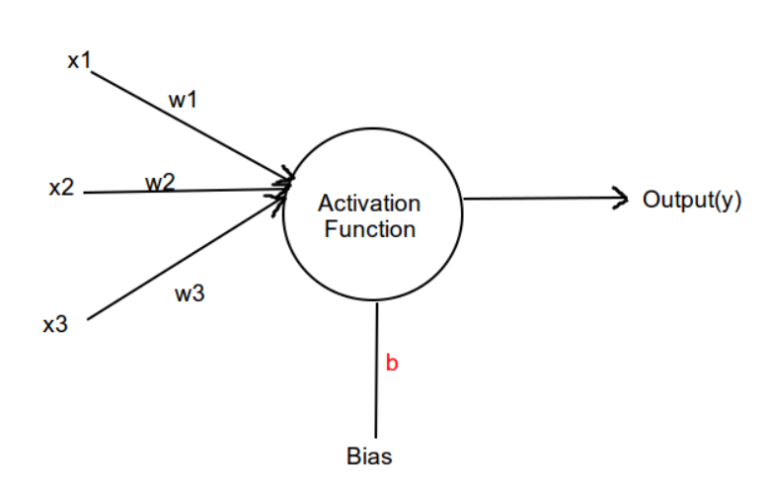
A Perceptron is essentially a binary classifier that helps separate data into two categories using a hyperplane. It consists of inputs, weights, a bias, and an activation function. The Perceptron takes input data multiplied by random weights and adds a bias to it. The weighted sum is then calculated by summing up the products of each input and its corresponding weight, along with the bias. This weighted sum is then passed through an activation function, which in this case is the unit step or Heaviside function. The unit step function returns 1 if the input value is greater than 0, and 0 otherwise.

Now, let’s discuss the steps involved in training a Perceptron. The process is simple and straightforward. Firstly, we need to initialize the weights and bias randomly. Next, we calculate the net input by multiplying the inputs with the weights and adding the bias. We then pass this net input through the activation function. If the predicted value is not equal to the targeted value, we update the weights and bias accordingly using the learning rate, which is denoted as alpha. The update formulas for the weights and bias are as follows:

wi(new) = wi(old) + alpha * error * xi
b(new) = b(old) + alpha * error

Next, we provide an implementation example that trains a Perceptron to predict the output of a logical OR gate. The code initializes the weights and bias, performs the necessary calculations, and updates the weights and bias based on the error. Finally, the trained Perceptron is tested with a sample input.

The implementation can be modified to train a Perceptron for other logical operations, such as AND, by changing the target values. However, when trying to classify non-linear problems like XOR, the Perceptron will not work effectively, regardless of the number of epochs trained. To solve this, we need to use a multi-layer perceptron with additional layers.

In conclusion, we have learned about the Perceptron and how to implement it from scratch in Python. While the Perceptron is a useful binary classifier, it can only handle linear problems. To handle non-linear problems, we need to use a multi-layer perceptron, which we will explore in the next part.